

Language:
Español
Subjects:
Flight 2(bis)
Flight 3(bis)
Theory
Other 'ballooners'
More theory:
Standard atm.
Calculator
Descent spd
These formulas are probably correct, but are not too useful to determine the total descent time: all are based on a constant air density (1.225 kg/m3) which is the density at 0 meters, and at 15°r;C. For a payload, falling from 30 km high, where the density is 150 times lower, and temps are 50 degrees below 0, the result is far from correct.
A few years ago I received through a publication, a graphic calculator (designed by the people at the University of Minnesota), which enables you to make a much more logical approximation to the problem: apart from weight and 'chute diameter, it takes into account the air density of the starting point. The result is the total descent time.
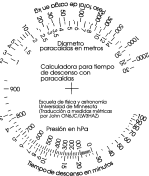 Here'sthat graphic calculator.
The link gives a .GIF (55k) with a resolution of 300 dpi, ready to be
printed, each disk separately.
Here'sthat graphic calculator.
The link gives a .GIF (55k) with a resolution of 300 dpi, ready to be
printed, each disk separately.
It's just a little impractical to have to know the pressure at the start of the fall, and, in these computerized times, those graphical things have lost some of their charm (though they do have their advantages!)
So, after some number juggling, I've derived a formula that takes into account:
MIND: All the formulas use metric units! (like hectoPascal (hPa), g in m/s², height in meters (m), etc.)
| Original formula - descent speed |
\(r=\sqrt\frac{2*g*W}{0.75*\rho*A}\) \(A=\frac{\pi*\rho^2}{4}\) |
| Descent time: |
First calculate
\(a_n=-20.0508+\frac{3.166*10^6}{h+57140}\) \(t=a_n*h*\sqrt{\frac{0.03*D^2}{W}}/60\) (minutes) |
Finally, I decided to make a slide calculator to determine:
Here's an image of the calculator: (Click to enlarge)
![]()
If you're interested in reproducing the calculator, here are 300 dpi images ready to be printed:
| (c) John Coppens ON6JC/LW3HAZ |